In this title behavior of volcanic gases is discussed due to the position of the Theory of Chain Reactions in magma and in the crater of a volcano. The theoretical account of the critical radius of the explosure of a crater is done.
It's known that 88-99,6% of the composition of gases accompanying the volcano are water steams [34], the rest 0,4 - 12 % form HCl, sulfurous gases (SO2, SO3 ), CO2, H2, H2S, N2, F2, Cl2, HF, HCl. Sometimes there can also be CH4, NH3, rodanic hydrogen, argon, other inert gases.
As soon as the main component of volcanic gases is water, so while discussing physical-chemical substitutions of those gases first we must pay attention to behavior despayed by water molecules in magma and separating from magma.
Practically it is impossible to follow the behavior water molecules in magma and in the crater of a volcano just with the help of observations [35]. It becomes the subject of the research after the eruption of the volcano.
Proceeding from Chain Reactions Theory it is possible to follow the behavior of water molecule before the eruption in magma and in the time of eruption in the crater of the volcano.
In acid, of middle acidity, and basic magmas behavior of water can be different. Basic laves, which contain 44 - 52 % SiO2 bellow 1100OC begin harden, mean while acid lavas owing to SiO2 great contents ( up to 75 % ) are still fluid in 700 - 750OC. Lavas of middle acidity take the middle position. The same concerns corresponding to magmas, so basic magma temperature must be appreciably high then the temperature of the acid magma. This represents that starting - point, which differs the behavior of volcanic gases ( so as water molecules ) in the basic and acid magmas.
Water perceptibly decomposes while being heated higher than 1500OC how it happens also under the influence of radioactive rays. High temperature as well as natural radioactivity exist in the earth's capsule. The reaction of water decomposition is the following :
2H2O = 2H2 + O2 ( 1 ).
Besides in 1200 - 1400OC CH4 and CO recover water:
CH4 + H2O = CO + 3H2.
CO + H2O = CO2 + H2.
Let's discuss the reaction of water decomposition in acid and basic magmas.
Variant 1: In the depth of acid magma exist high ( T> 1500OC ) temperatures. In that case, ( 1 ) balance is moved to the right, water, which is in magma, is completely or partially dissociated to hydrogen and oxygen. Magma, lifting to the earth's surface, gradually freezes, as a result of which the reaction of water disintegration is breaking. In the depth of magma the reaction of water synthesis doesn't also go through, because each molecule of hydrogen and oxygen is surrounded by tens and hundreds of molecules of substances which form magma and the probability of the meeting and reactioning of hydrogen and oxygen is little.
When magma reaches the earth's surface and turns into lava, gases diluted in it begin to separate like bubbles in rapid way. In each bubble appear hydrogen and oxygen in 1 : 2 correlation. Each bubble presents itself like spherical reactor full with hydrogen - oxygen mixture.
The water synthesis taken place in bubbles. Bubbles, which are full with hydrogen and oxygen become bubbles which are full of water steam. As soon as:
2H2 + O2 = 2H2O( 2 ).
33,3 % diminution of cubic capacity takes place during the reaction, so the sizes of bubbles diminish so many times as the cubic capacity. It pulls a kind of concentration of lava capacity out.
Variant 2: Acid magma has low temperature in its depth. Water, containing in magma, doesn't turn into hydrogen and oxygen, reaches the earth's surface and then passes to the environment.
As difference to the previous case, in this one the external layer of lava is cold as in the previous case it was heated owing to the separated temperature of the reaction of the water synthesis.
In basic magmas, the representation is different because the temperature of the basic magma is appreciably high in general, than the temperature of acid magma [35]. In those kind of conditions, water is completely or partially disintegrated to hydrogen and oxygen [36].
While magma lifts, its temperature decreases, though nevertheless, it remains higher then the temperature of acid magma.
In the layer, which is close to the earth's surface, the part of hydrogen and oxygen turns into water and the other one goes to the gas capacity ( crater of the volcano ). Just near the surface of lava the reaction ( 2 )goes in the most intensive way. The increase of gas phase temperature in that part must be explained by that [35]. For example, on the bottom of the lake ( 11m ) there is 1180OC and in the flame which has 4m height there is 1350OC or the temperature of lava is T = 1150OC, meanwhile the temperature of the forcing fire on the lake is 1400OC. Due to the circumstances, the combustion of hydrogen can take place by slow reaction as well as in the self-kindling sphere [37]. Due to the representation of kindling peninsula, the combustion had to go through with explosure, though presence of perceptible numbers of water steams can prevent it and the reaction can have quiet process. In the case of quiet process, lava flows out quietly from the crater.
The representation changes if the combustion of hydrogen takes place not by the slow reaction, but by the self-kindling one. In that case , explosive phenomena take place in the crater, about which the following affirmation testifies [35] " Being near the mouth of the crater, dull explosions and thunders, which reminds a thunderstorm can be heard from the depth, which come from the depth and are accompanied by the light shock of soil. The explosure of slays as if flowing out follows it immediately and they erupt out the eddies of the steam a few seconds later".
Let's discuss the case of explosion. The crater of Prihnukargigur extinct volcano in Island is taken as the crater - reactor ( Figure 45 ) [38].
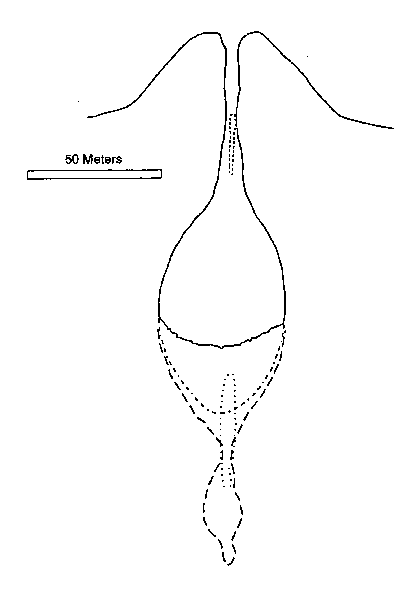
Figure 45. Prihnukargigur extinct volcano crater in Island.
We observe it first approximately like with a cylindrical capacity 25 meter radius ( R ) and 70m height (h ). The capacity of the cylinder is calculated by the following formula:
V = p . R2 . h = 3,14 . (25 )2 . 70 = 1,4 . 105m3.
Let's accept that the reactor - crater is completely full of 2 : 1 correlation oxygen : hydrogen ratting mixture. It forms 0,93 . 105m3 H2 and 0,47 . 105m3 O2. Due to Avohadro`s law in the normal circumstances ( P = 1 atmosphere, T = 273OK ) 1 mol of any gas occupies 22,4 liter ( 22,4 . 10-3 m3 ) capacity. Consequently, in the normal circumstances of gases, weight quantities containing in the crater will be:
hydrogen - ( 2 .0,93 . 105 ) : ( 22,4 . 10-3 ) = 8,3 .106 gram = 8,3 ton or 4,15 . 106 mol.
oxygen - ( 32 . 0,47 . 105 ) : 22,4 . 10-3 = 67 .106 gram = 67 ton or 2,09 . 106 mol.
In the tame of eruption, in the crater the temperature of gases is much higher than the room temperature (~300OK ). The concentration of ideal gases decreases in the unit capacity by the equation of ideal gases condition because of the increase of temperature [7]:
PV = RT,
where P- is the pressure of gas, V- is its volume, T-is the temperature, R-is the gas constant.
For real gases the equation of the condition has following look [39]:
( P + a/V2 ) . ( V - b ) = RT.
a and b are the constant values for given gas.
For the clarity of calculation it is comfortable to make use of the equation of the condition of ideal gas ( PV = RT ). In that case, the dependence of the gas volume on temperature is defined by the following formula:
Vi = ( R . Ti ) : Pi.
In the same way, the gas volume in normal conditions ( PO = 1 atm. TO = 273OK or 0OC ) is defined by the following formula:
VO = ( R . TO ): PO.
Let's accept for clarity that while lifting the temperature in the crater, the pressure of gases remains invariable. It is acceptable because the crater interacts with the environment, what tries to attain the pressure of the crater to equalize to the pressure of environment. In that case, in Ti temperature the expansion of gas volume will form:
Vi = ( VO . Ti ) : TO.
If, for example, Ti = 773OK ( 500OC ), in that case Vi = ( VO . 773 ) : 273 = 2,83 . VO.
Then, while heating gases from 273OK ( 0OC ) to 773OK ( 500OC ), their volume expands 2,83 times. It means that in 500OC in the same volume contain 2,83 times less gas molecules than they were in 0OC. Consequently, H2 and O2 those quantities, which we got for the crater mentioned above are necessary to diminish 2,83 times. Gases quantities correspondingly become:
hydrogen - ( 4,15 .106 ) : 2,83 = 1,46 . 106 mol,
oxygen - ( 2,09 . 106 ) : 2,83 = 0,74 . 106 mol.
While heating the hydrogen - oxygen mixture ( H2 : O2 = 2 : 1 ), setting fire to it or illuminating it strongly, the mixture explodes [42]. Let's count the energy separating during the explosion of gas mixture accumulated in the crater of the volcano. The explosion if fulfilled by the following thermo-chemical equation:
2H2 + O2 = 2H2O + 572,5 kJ ( 136,74 kcal ). ( 2 ).
As it is seen from ( 2 ) thermo-chemical equation, during the combustion of each 2 mol of hydrogen 572,5 kJ energy separates. Hence during the combustion of 1,46.106 mol of hydrogen the separated energy will be:
( 572,5 . 1,46.106 ) : 2 = 417,9 . 106 » 4,2 . 108 kJ.
Let's count the trotil equivalent of the explosion. The temperature of 1 kg trotil ( trinitrotoluol ) explosure equals to 4190 kJ. Hence the trotil equivalent of the explosion of 1,46.106 hydrogen will be:
( 4,2.108 ) : 4190 » 1.105 kg = 100 ton trotil.
So, the power of the sxplosure of the ratting mixture in the crater equals to ~100 tons of trotil explosion power.
In order to estimate the destructive power of trotil for chopping up rocks we did the following experiment. We prepared from the melted basalt 3 cylinders with 8 sm. diameter and 12 sm. height, then we filled each of them with 25 gram trotil and exploded them in the special cabin for explosion. The sizes of the cabin for explosion are 10 m, height, the diameter of the base 8 m ,the thickness of the walls 1 m, concrete. From the inner side, the dome and the bottom are covered with steed strips of metal which have 10 mm thickness.
With the goal of determining the sizes of occurring debris, there were situated with 1 mm thickness steel then strips of metal round the experimental cylinder in a distance of one meter. Imprints of debris occurring from the explosion had to be branded on them ( Figure 46 ).

Figure 46. The structure of the cabin for explosure: 1- the cabin for explosure, 2 - strip of metel, 3 - cylinder.
We discovered the imprints of three debris with ~1 sm diameter on the on the thin strips of metal which have 1 mm thickness in only one of three explosions we did. Several tens of debris had 0,1- 0,3 mm diameter and the rest whole mass of the rock turned into so small debris, which couldn't leave an imprint on the strip of metal of 1 mm thickness.
So, the experiment showed, that 25 gram of trotil will be enough for turning the basalt mass with ~600 mm3 capacity into the smallest debris. And will the mountain which has the crater, which is represented in Figure 1 explode if the rattling mixture, accumulated in its crater, explodes during the eruption. As it is seen from [6], the mountain presents itself as a truncated cone. The volume of the truncated cone is clearly defined by the following formula:
V = [p ( R2 + r2 + R . r ) . h] : 3
The diameter of the base of the mountain ( R ) is ~40 m, the diameter of the peak ( r ) is ~ 20 m, the height ( h ) is ~36 m. The volume of the cone-mountain will correspondingly form:
V = [3,14 . (402 + 202 + 40 . 20 ) . 36] : 3 » 1.105 m3.
If 25 gram ( 2,5 . 10-5 t ) trotil chops up ~600 sm3 capacity basalt, then 100 tons will chop up:
[6.10-4 . 100] : ( 2,5.10-5 )= 2,4 . 103 m3.
If 25 gram ( 2,5.10-5 ton ) trotil chops up ~ 600 sm3 volume basalt, then 100 tons will chop up 2,4.103 m3. Meanwhile, the volume of the crater cone is 1 .105 m3. Then if only the crater like that is completely full with the rattling gas, it will not explode.
But, there are some cases of the explosion of crater in nature. With the help of the method, mentioned above, the united formula can be found, which will allow to say beforehand that which of the volcanoes, which have the crater of that type, which is presented in Figure 45, can explode and which of them cannot.
Let's indicate the temperature of gases of the crater - T, the volume of the crater - V. Bringing to the normal conditions the volume of the rattling mixture containing in the crater will become:
VOW = ( V . TO ) : T.
The thermal energy separated by the reaction ( 2 ) - Q for VOW volume will be:
Q = ( 8,5 . V . TO ) : T.
For this quantity of separating energy the trotil equivalent will form:
T. E. = ( 2.10-3 . V . TO ) : T.
The volume of the rock chopped up by 1 kg trotil we mark by a ( m 3 ). a- is a constant value, but it has different values for different rocks. In that case,
[( 2.10-3 . V . TO ) : T] kg trotil equivalent explosure will chop up the rocks with the following volume:
V1 = [( 2.10-3 . V . TO ) : T] . a.
The upper part of the mountain, which has probability to explode, is like a truncated cone which volume is defined by the formula:
V2 = [p ( R2 + r2 + R . r ). h] : 3.
If we take the statements , which were said up to the present, as the basic, the crater of the volcano will explode if
V1 > V2, or
[( 2.10-3 . V . TO ) : T] . a > [p ( R2 + r2 + R.r ) . h] : 3. ( 3 ).
This equation is possible to show up clearly as soon as R is several times more than r, V2 can be accepted as the volume of the cone, so:
V2 = ( p . R2. h ) : 3.
In that case the expression ( 3 ) will get more clear look:
[( 2.10-3 . V . TO ) : T] . a >[( p . R2 . h ) : 3].
[( 2 .10-3 . V .TO ) : T] . a > R2 . h . ( 4 ).
For the form of the crater presented in Figure 45:
V = ( p . R2 crater . h ) : 2.
In that case the expression ( 4 ) will get more clear look ( TO = 273OK ):
2.10-3 .[( p . R2 crater . h ) : 2] . TO . T-1 . a > R2 . h.
3,14.10-3 . R2 crater . 273 . T-1 . a > R2 mountain.
857.10-3 .
( 0,8 . R2 crater . a ) > R2 mountain.
R crater > R mountain [T :( 0,8 . a )]0,5. ( 5 ).
( 5 ) expression gives the value of that critical radius of the crater, in the case of which the crater in the tame of the eruption of the volcano is subjected to explosion.
So employment of chemical kinetics and specifically employment of the theory of Chain Reactions, in the time of volcanic phenomena gives the quite concrete values to the phenomena of the separation of gases. We are sue, that the use of the states of chemical kinetic in the volcanospeleology can give the explanation of the physical-chemical phenomena, which happen with the volcanic gases.