Activities of volcanoes have a special place in a number of physics - chemical phenomena proceeding on the earth. It is one of the main factors forming the surface of the earth. Volcanoes are attributed to the world disasters. Volcanoes are not special phenomena only for the earth. The imprints of volcano vigorous activity were discovered on the other planets of the Sun’s system specifically on Mars, Mercury and Venus [40]. All these things make the research of volcano activity modern and urgent.

Volcanoes are those strong phenomena, which act on the earth, which formation whole process take place in the environment not available for on immediate research. And if we make the danger connected with volcanic eruption research in a short distance into consideration, it will be clear how many valuable data will have laboratory researches of the volcanic process for investigations. But high temperatures and pressures bother the simulation of volcanoes and their physics - chemical researches realization in the laboratory conditions. What follows everything that was said is how important is the simulation if not of the whole volcanic activity then, at least, the simulation of a part of it.

We suggest the RFKM for the simulation of that kind of phenomenon [42]. The method is useful for a number of researches of gas phase chemical reactions. We came to the conclusion that it can be used for those displays of a volcanic activity which are the chemical reactions proceeding in volcanic gases, the periodic separation of volcanic gases and the changes of thermal balance taking place in the moment of the separation of gases from magma.

Radicals taking part in chain reactions proceeding in gas phase and the chemical combinations ( H₂O, H₂, H₂S and others ) containing in the volcanic gases, prove that that kind of reactions, which take place there, are strictly unstable combination. In reality, their each duet or trio collision to each other or to other molecules and atoms becomes the cause of radicals destruction or appearance of new radicals.

Duration of radical life is directly comparable to existing radical till the first collision period of time, we mean, the length of free run, which is decided by the following formula [39]:

l = 0,057 : ( r² . n )

n - is the number of particles in the united volume, r - is the radius of patticle.

As it seem from the formula l ~1 / P, so the pressure ( P ) diminution increases the life duration of radicals. This is the main idea in the base of RFKM.

The second idea is, that such active particles as hydrogen atom ( H ), alkyl radicals (CH₃, C₂H₅ and others ), halogen atoms ( Cl, Br... ) and others have time to be recombined even with the small quantity of oxygen existing in the system and form the peroxide kind of radical HO₂ or RO₂, where R = CH₃, C₂H₅,.., HlO₂ ( Hl = Cl, Br, J )under even very small pressure. These are comparably more stable radicals then those radicals and atoms from which this peroxide kind of radicals appeared. From the other side and they also take an active part, proceeding in the chemical process. The RFKM investigates the behavior of these radicals.

Usually, the concentration of peroxide kind radicals in gas phase is low from the border of sensitivity of research devices. But peroxide radicals can be frozen in the temperature of fluid nitrogen with the frozen matrix. It gives the opportunity to accumulate radicals in big quantities and because peroxide radicals have single electron, they can be discovered with the help of the phenomenon of Electronic Paramagnetic Resonance ( EPR ).

In the flow-production circumstances the realization of reactions proceeding in the gas phase is a good model for the reactions proceeding in volcano gases. The reactor, represented on figure 47, serves as that volume where the simulated reaction proceeds.

In the gas phase, the radicals concentration ( C₁ ) is decided as the alignment of accumulated radicals number ( R particle . sec.^-1 ) and gas shield volume speed ( W cm³.sec^-1 ):

C₁ = R : W.

The radicals concentration in the reactor:

C₂ = ( C₁ . P₂ . T₁ ):( P₁ . T₂ ),

where T₁ and P₁ are temperature and pressure after the capillary ( T₁ » 300 ^oK, P₁ = 10^-3 - 10^-1 tor ) and T₂ and P₂ are temperature and pressure in the reactor ( magma ) ( T₂ = 1000 - 1300^OK, P₂ = 760 tor ).

The gas mixture, which imitates the gas mixture erupting from a volcano crater in the moment of separation from magma, they enter the reactor made of the quartz glass, which can give warmth up to ~1300^OK with the help electric furnace under the pressure of environment. The reacted gases flow out from the other end of the reactor. They imitate the volcano gases, which changed their composition with reactions and their correlation with the environment. The last one value, which is decided precisely changing the gases composition which enters the reactor we can find that correct combination of gases, when the gases composition, which go out from the reactor coincide precisely with the volcano gases composition mixed with the environment. That precise combination, which is found, is the volcanic gases composition in the instant of its separation from magma.

As soon as we find the correct concentration of volcano gases separating from magma the kinetic investigation of a simulated reaction begins. The research of gas fluid of the reaction, and, perhaps, of the strong substances takes place in the gas shield going out of the reactor.

It is necessary for volcano gases to distinguish two kinds of reactions which are different in principle. The first type is evaporating combinations reactions in the fluid phase ( alloy ) and high temperatures, dissolved in silicate alloy containing in magma, in the earth’s capsule. Here, the molecules of gases are in a number of difficult balance interactions: gas - gas, gas - silicate alloy, gas - strong rocks. This stage is difficult to simulate.

Volcano gases begin interactions with each other and the environment after separation from the fluid phase. The sharp temperature fall promotes according to the realization of exothermic reactions by Acting Tract Law.This part of the reactions can be simulated with the help of RFKM between volcano gases and air components ( first with oxygen, also perhaps nitrogen ). On the contrary to RFKM, where the temperature fluctuations on the whole length of the reactionary sphere don’t exceed ± 0,5^OC, it is necessary to have the reactor with temperature gradient for the reactions simulation proceeding in volcano gases. The temperature of the reactor entrance must be 1000^OC ( the temperature of volcano gases in the moment of the separation from lava ) and its exit temperature must be approximately the same as it is in the environment (Figure 47).

Figure 47. The device for the simulation of the reaction proceeding in volcanic gases: 1- the reactor, 2 - the electric furnace, 3 - capillary, 4, 5 - freezing unit, 6 - the sounding board of Electron Paramagnetic Radio-spectrum-meter ( EPR ), 7 - EPR magnet.

Let’s think that, the volcano gases erupted from a crater reach 1 km height in one minute. In that period of time the gases temperature falls from ~1000 ^OC to environmental and the linear speed of gases motion equals 10² m/sec.

D T = 1000 ^OC temperature difference can be obtained in the reactor with approximately 1 m length in experimental way. If the diameter of the reactor is 1 mm, and the volume speed of gases flowing in it is several litter/sec, the the same 10² m/sec. linear speed will be secured, which is in the speed of volcano gases motion after eruption in the environment. The reactions, proceeding in volcanic gases, can be simulated completely in that kind of the capillary reactor.

The next task, which can be solved with the help of RFKM, is the simulation of the thermal regime change taking place in the moment of volcanic gases separation. How the measurings show, the temperature deviations can be and they can influence essentially on the mechanism of the volcano eruption.

The phenomenon of eruption is the mainest peculiarity of volcanoes activity. It is represented in the following way [35] in general lines. It is necessary to know the connection between the internal ( in magma ) and external pressure in order to understand the volcanic activity. Theoretically, the balance between them could be confirmed only in the case when the piromagma, which is the condition of magma oversaturated with gases, bubble or even foam, which is saturated with gases in the same volume everywhere and if the pressure of equal steam prevails everywhere in hypomagma. Hypomagma is with gas and can exist only when the pressure is more than the pressure of the steam of molecular dissolved gas.

The condition lice a balance can be only in the case, if magma stays in quiet condition and if the free gas phase evaporated completely from the piromagma. Though the condition lice quietness in less possible as magma gives its warmth from the surface and to the distance surrounded in contacts and becomes strong. So the hydrostatic balance is violated and the convection flows begin.

Piromagma, saturated with gas lifts and enter the sphere of lower pressures, where it becomes oversaturated and separates the free gas phase. The formation of bubbles speeds up degasation on the surface of magma and push the powerful double phase convection forward. Coming down epimagma, because of the low pressure of steam, is in the balance condition with deep magma. ( Epimagma is magma, which is degasated strongly and not epurated or identical to the not erupted yet lava ) The balance recovers because of the gas diffusion and epimagma, which corresponds the depth, recovers to piromagma or hypomagma. Though it is necessary for the long lasting diffusion lifting of gases from the depth of a hearth. This kind of degasation phenomenon is the cause of the volcanic activity on the earth.

Magma degasation with its physical character is close to the process of RFKM which takes place in the Duar vessel. In one case, volcanic gases ( 88 - 99,6% water foams ) separate from magma silicate alloy and the gas nitrogen separates from the fluid nitrogen in the other case. The separation has some periodicity. The Strombolic type eruptions are especially famous [35], which take place with equal intervals and gases coming out of the crater separate from magma with equal periods. It was necessary for the research of the process, which accompanies the separation of gases from magma, to simulate that periodic separation of gases.

As the experiments showed, in the RFKM Duar vessel in certain circumstances, it ispossible to realize the process approximately the same as the periodic separation of volcanic gases. In certain circumstances, we were success to create such conditions, when gas move from the fluid phase ( nitrogen ) not constantly but with periods which equal 2,5 - 3 minutes. That kind of special condition can be preserved for a long time.

The phenomenon of the gas separation creates power changes in the fluid phase ( in the crater or Duar vessel ). In order to estimate the kind of changes we measured temperature changes, which take place during the time of RFKM vibrations. We worked the special construction of Duar vessel out with that goal, which is represented in Figure 48.

Figure 48. The scheme of Duar vessel: 1 - matrix, 2 - thermocouple, 3 - seam of thermocouple, 4 - thread.

The pressure in Duar vessel partition made 0,2 - 0,3.10^-3 tor. The liquid nitrogen ( - 196 ^OC ) was a freezing substance in RFKM freezing unit. The temperature of the matrix was measured with the cooper - constant thermocouple ( d = 0,1 mm. ), which union was strongly connected with the tip of Duar vessel finger. The thickness of the tip wall is ~ 0,5 mm. The matrix covered the lump of the thermocouple in all experiments, which diameter is ~ 0,3 mm. The thickness of the matrix didn't exceed 2 mm. In order to prevent the thermocouple motion in the matrix, it was fix with glass thread in a distance 10 mm from the union. The curve of the degree, which shows the connection between the contact difference of thermocouple potential and temperatures was displayed in the experimental way.

In order to separate the thermocouple from the external influence, we put the substances: H₂O, H₂O₂, CH₃CO₃H, C₂H₅OH, coal, organic resin, which are different in their physical - chemical characteristics, on the thermopair under the vacuum. How the measuring showed, all the substances satisfy the standards of separation.

We managed to registrate the temperature changes which take place in the moment of the gas periodic separation with the help of the thermopair. To our point of view, ascillations are the result of double physical and chemical phenomena. Only physical development of the phenomena is presented here.The results are shown in the Figures 61, 62 and 63.

Figure 49. The variant of the experiment of periodic freezing of Duar vessel tip: (D T » 10^O ), P = 3.10^-2 tor.

Figure 50. The variant of the experiment of periodic freezing of Duar vessel tip: (D T » 7^O, P = 1.10^-1 tor.

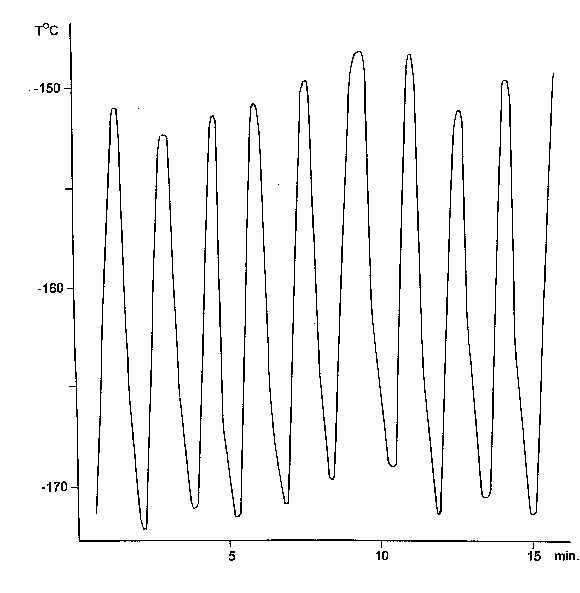
Figure 51. One of the experiments of periodic freezing of the Duar vessel tip registration with the help of the automate device ( D T » 20^O ).

The measurings give the opportunity to estimate that heat, which is taken from the environment when the gas separates from the fluid phase. It is calculated by the following formula:

Q = C_p . m .D T

C_p - is the quartz specific thermal capacity calorie/gram.degree, m - is the freezing mass, in the case the end of Duar vessel finger ( ~ 1 gram ), D T - is the difference of measured temperatures. In the 50 - 100 ^OK intervals C_p » 0,08 calorie/gramm.degree[63]. In the experiments we got D T is up to 20^O (Figure 51 ).

The heat taken from the Duar vessel finger will be:

Q = 0,08 . 1 . 20 = 1,6 calorie.

So each bubble which is separated from the fluid nitrogen, takes 1,6 calorie warmth from the environment.

The weight of N₂ - one bubble will be in normal condition ( in 273 ^OK ):

28 : ( 22,4 . 10^-3 ) = 1,25 . 10^-3 gram.

The calculation of the same bubble weight in the temperature of the fluid nitrogen ( 77^OK ):

T₁ : T₂ = 273 : 77 = 3,54

1,25 . 10^-3 . 3,54 = 4,4 . 10^-3 gram.

So 4,4 .10^-3 gram nitrogen ( one bubble ) takes 1,6 calorie of warmth from quartz.

In the case of H₂O one bubble, the calculation of warmth taken from the environment, we decide from the values of N₂ and H₂O, C_p. The values we have are the following [63]:

For N₂ in 1000^OC C_p = 0,29 ( P = 1 atmosphere ),

For H₂O in 740^OC C_p = 0,55 ( P = 1 atmosphere ),

C_p^H2O : C_p^N2 = 0,55 : 0,29 = 1,9.

In the case of H₂O one bubble the warmth taken from the environment will be:

1,6 calorie . 1,9 = 3,04 calorie.

One bubble of water steam is so many times lighter than N₂ one bubble as H₂O molecule is lighter than N₂ molecule:

M_H2O : M_N2 = 18 : 28 = 0,64.

One bubble weight of water steam will be:

4,4.10^-3 . 0,64 = 2,8.10^-3 gram.

So 2,8.10^-3 gram of water steam fluid separating the environment takes 3,04 calorie warmth.

In nature this phenomenon takes place in large quantities, when tens and thousands ton of gases ( water steam in general ) are thrown away to the environment every time. Extrapolating the laboratory experiments it is possible to estimate the absorbtions of warmth which take place in the moment of periodic separation of volcanic gases.

Let’s accept symbolically that the number of separating water steam is 10 ton. The warmth taken by 10 ton ( 10⁷ gram ) of water steam will be:

( 3,04 calorie . 10⁷ gram ) :( 2,8 . 10^-3 gram )= 1,1.10⁷ kilocalorie.

The calculation of the volume of 10 ton water steam:

( 22,4 litre. 10⁷ gram ): 18 gram = 1,24.10⁷ litre = 1,24.10⁴ m³ ( normal conditions: T = 273 ^OK ).

The volume of 10 ton water steam change into normal conditions ( T = 273 ^OK ) will be 1,24.10⁴ m³.

The 10 ton water stream volume will increase T₂ : T₁ times at 1000^OC. So:

T₂:T₁ = ( 1000 + 273 ):273 = 4,66 at 1000^OC ( the symbolic temperature of magma ).

The volume of 10 ton steam will be:

1,24.10⁴.4,66 = 5,8.10⁴m³.

So 10 ton volcanic gases ( water steam ) existing in degasation magma take 5,8.10⁴ m³ (~40 . 40m. 40m³ ) volume in the crater of the volcano. Or if the crater diameter is 100m and the surface S = p r² = 3,14.( 50 )² = 7500 m², will have ~8m height foam of the surface of magma: ( 5,8.10⁴ : 7500 » 8 ).

Now let’s calculate, how much magma is frozen at the same time in the process of 10 ton volcanic gases eruption at the same time when 1,1.10⁷ kilocalorie warmth is taken from the environment ( magma ). Let’s consider the diameter of volcanic gases bubble 1 centimeter:

V = 4 /3 p r³ = 4 . 3,14 . ( 0,5 )³ = 0,52 cm³ = 5,2 . 10^-7 m³.

The calculation of bubbles number is:

N =( 5,8 .10⁵ ): ( 5,2 . 10^-7 )» 1,1 .10¹²

The calculation of the volume and weight of the bubble capsule:

Let’s consider the thickness of the bubble 0,01 mm. In that case, the volume of the bubble will be calculated as the difference of two lumps volumes, for one of which r₁ = 5 mm and for the other r = 5 - 0,01 = 4,99 mm.

V₁ = 4 . 3,14 . ( 0,5 )³ : 3 = 0,5233 mm³

V₂ = 4 . 3,14 . ( 0,499 )³ : 3 = 0,5191 mm³.

D V_i = V₁ - V₂ = 0,5233 - 0,5191 = 0,0042 mm³.

D Vi = 4,2.10^-3 mm³.

The volume V taken by the capsules of all bubbles:

V =D V_i . N = 4,2.10^-3 . 1,1.10¹² = 4,6.10⁹ mm³ = 4,6.10⁶ cm³.

The total weight of the bubbles capsules will be:

P = d_magma . V

For magma d » 2,9g/cm³ [35].

P = 2,9 . 4,6.10⁶ = 13,34.10⁶ gram = 13,3410³ kg

P » 13 ton.

How the measurings show 10 ton volcanic gases, separating from magma, take ~1,1.10⁷ kilocalorie warmth, freezing the bubbles capsules, which total weight is ~13 ton. Now we can count what degree the whole part of bubbles capsule freezes. It is decided by the following formula:

Q = C_p . P . D T

We don’t have C_p for magma. We use represented in [63] a number of strong substances alloys from C_p values which have ~10 klcal value. Let’s accept the same volume of magma: C_{p »} 10 calorie/gram. In that case the volume of D T will be:

D T = Q : ( C_p . P ) = 1,1.10¹⁰ calorie : ( 10 cal/gram . 13 . 10⁶ gram )

D T » 100^O.

So 13 ton part of bubbles capsules, in the moment of separation of 10 ton volcanic gases, freeze up to ~100^O immediately. It can forms the additional phenomenon of separation of minerals from magma.

The value of the bubble separating from magma depends on the stickiness of magma, its density and others. If the diameter of the bubble is 3 cm ( 30 mm ), the corresponding calculation give:

N =( 5,8 . 10⁵ ): ( 1,4 .10^-7 ) = 4 . 10¹⁰ pieces.

r₁ = 15 mm, r₂ = 14,99 mm.

V₁ = 4 . 3,14 . ( 15 )³ : 3 = 14175 mm³.

V₂ = 4 . 3,14 . ( 14,99 )³ = 14146 mm³.

D V_i = V₁ - V₂ = 14175 - 14146 = 29 mm³.

V = D V_i .N = 29 . 4 .10¹⁰ = 1,16 . 10¹² mm³ » 1 .10⁹ cm³.

P = d_magma . V = 2,9 . 1.10⁹ = 2,9 . 10⁹ gram = 2,9 . 10⁶ kg = 2,9 . 10⁶ t.

D T = Q : ( C_p . P ) = 1,1 . 10¹⁰ : ( 10 . 2,9 .10⁹ ) = 11 : 29 » 0,4^O.

T» 0,4^O means that the freezing of magma, which forms the bubbles capsule in the moment the separation of bubbles doesn’t take place in fact. The reason is the big part of bubbles capsule ( 2,9 .10³ ton ).

Considering the simulation of the separation phenomenon of gas from the fluid phase with RFKM as the base, we get the following united formulas for the part of freezing magma and its freezing size:

The warmth taken by M part volcanic gases from magma:

Q = 3 M : ( 2,8 . 10^-3 ) calorie.

The gases volume in T^O K ( in magma temperature ):

( 22,4 . M . T₂ ) : ( 18 . 273 ) = 4,5 . 10^-3 . M . T₂ litre.

One bubble volume:

V_i = 4p r³ :3, where r - is the radius of a bubble.

A number of bubbles:

N = ( 4,5 . 10^-3 . M . T₂ . 3 ) :( 4 . p . r³ )= ( 1,1 . 10^-3 . M .T₂ ) : r³

One bubble capsule volume:

D V_i = 4p [r³ - ( r - 0,001 )³] : 3 = 4,2 [r³ - ( r - 0,001 )³].

The sum of the volume of all bubbles capsules:

V = D V_i . N = 4,2 . [r³ - ( r - 0,001 )^3] .[( 1,1 . 10^-3 . M . T₂ ) : r³]

The total weight of freezing magma at the moment of gases separation:

P = d_magma . V = { 4,6 . 10^-3 . [r³ - ( r - 0,001 )³] . M . T₂ . d_magma } :r³ (1).

The total freezing of bubbles capsule:

D T = Q:(C_{p magma}.P)=3r³ : { 2,8.10^-3.C_{p magma}.4.6.10^-3[r³-(r-0,001)³].T_mag.d_magma }

D T = 2,3.10⁶.r³ :{ C_{p magma}. [r³-(r-0,001)³].T_magma.d_magma} . ( 2 ).

The part of freezing magma ( P ) and the size of freezing (D T ) is calculated at the moment of gases separation with the help of formulas ( 1 ) and ( 2 ).

It is possible to decide, which minerals and in what quantity separate at the moment of magma degazation by knowing those two values.